GatorSheavesMutably | 13 февраля 2021 ### Группа точек на эллиптической кривой в криптографии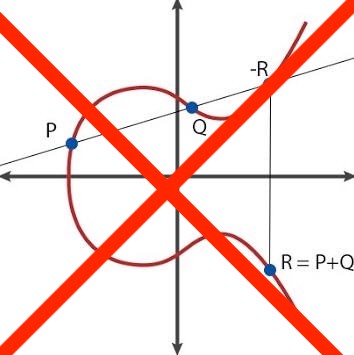 

#### План доклада * Зачем криптографам группы * Конечное поле $\mathbb F_p$ * Плохая группа $\mathbb F_p^*$ * Хорошая группа $E(\mathbb F_p)$ * Проективная плоскость $\mathbb P^2_{\mathbb F_p}$ * Групповой закон * Основные свойства * Ассоциативность

#### Что такое (абелева) группа Множество $G$ с операцией $\oplus$ такой, что: * замкнутость * $x \oplus y \in G$ * коммутативность * $x \oplus y = y \oplus x$ * $\{\mathcal O\}$ — нейтральный элемент * $x \oplus \{\mathcal O\} = x$ * $\bar x$ — обратный к $x$ * $\bar{x} \oplus x = \{\mathcal O\}$ * ассоциативность * $x \oplus (y \oplus z) = (x \oplus y) \oplus z$

#### Дискретный логарифм в G * *Антон* выбирает $g \in G$ — генератор * $g, g \oplus g, g \oplus g \oplus g, \ldots$ генерирует всю $G$ * *Антон* загадывает случайный $k \in [1,|G|]$ * *Антон* публикует $h = \underbrace{g \oplus \ldots \oplus g}_{k}$ * *Егор*, знающий $h$, в хорошей $G$ не может восстановить $k$ за разумное время

#### Два дискретных логарифма в G * *Антон* загадывает $k_a$, $h_a = \underbrace{g \oplus \ldots \oplus g}_{k_a}$ * *Вадим* загадывает $k_b$, $h_b = \underbrace{g \oplus \ldots \oplus g}_{k_b}$ * *Антон* и *Вадим* обмениваются $h_a$ и $h_b$ * *Антон* вычисляет $h_{ba} = \underbrace{h_b \oplus \ldots \oplus h_b}_{k_a}$ * *Вадим* вычисляет $h_{ab} = \underbrace{h_a \oplus \ldots \oplus h_a}_{k_b}$ * *Егор* знает $h_a$ и $h_b$, но не знает $h_{ab}$ и $h_{ba}$

#### Что такое поле Множество $F$ с операциями $\oplus$ и $\odot$ 1) $\oplus$ — группа над $F$ 2) $\odot$ — группа над $F$ (но без нейтрального для $\oplus$) 3) $(x \oplus y) \odot z = (x \odot z) \oplus (y \odot z)$ Бесконечные поля: $\mathbb{C}, \mathbb{R}, \mathbb{Q}, \ldots$

#### Конечное поле $\mathbb F_p$ Для простого $p \in \mathbb{N}$ * $F = \mathbb{Z}/p\mathbb{Z}$ * $\oplus = +, \odot = *$ В примерах используем $\mathbb{F}_{41}$ * $20 + 22 = 1$ * $-20 = 41 - 20 = 21$ * $\frac{1}{20}= 39$

#### Плохая группа $\mathbb F_p^*$ <div style="border: 5px solid black"> $p$ — 2048 бит $2^k \equiv h \mod p$ $k$ = ? </div> $h = $ <div style="word-wrap: break-word; font-size: 24px;">12233204741278037113413334644622357352316093577983348160885552823554063444178268426936171188787496171281364566153284172743042082376688378797084515428514957854827263478944147254682266384676686912781627231522029218920934456888709824417854506048331268075650588363199443351045431810917872933640031185788580783165655336883324913657765633896314393575705165706977825910395897670080231457670050070815023873467593079107896781325755667733744398157124761326956502003112471355484298729855692601624182095627869888467043691726041081331943390507951904378428727090146664578581570076051464291703661213796234509051525652376738106854329</div>

#### Хорошая группа $E(\mathbb F_p)$ <div style="border: 5px solid black"> $p$ — 256 бит $[k]g = h$ $k$ = ? </div> $h = $ <div style="word-wrap: break-word; font-size: 24px;">271958093091073061223011692103281126119346280182596018712398146965375344803488</div>

#### Проективная плоскость $\mathbb P^2_{\mathbb F_p}$ <div style="font-size: 22px"> Элементы — классы эквивалентности над $(x, y, z) \in {\mathbb F_p}^3$ (но без $(0, 0, 0)$) $(x, y, z) \simeq (kz, ky, kz), k \in {\mathbb F_p}$ </div> <div style="float: left">  </div> <div style="font-size: 22px"> Представители: * <span style="color:blue">$z \neq 0$</span>: $(x, y, z) \mapsto (\frac{x}{z}, \frac{y}{z}, 1)$ * <span style="color:green">$y \neq 0$</span>: $(x, y, 0) \mapsto (\frac{x}{y}, 1, 0)$ * <span style="color:red">$(x, 0, 0) \mapsto (1, 0, 0)$</span> </div>

#### Кривые в $\mathbb P^2_{\mathbb F_p}$ Корни многочленов $F(x, y, z) = 0$ Многочлены гомогенные * $F(kx, ky, kz) = k^{deg(F)}F(x, y, z)$ * имеют мономы вида $x^i y^j z^k, i + j + k = deg(F)$ Нам понадобятся только * прямые * $L(x, y, z) = ax + by + cz = 0$ * эллиптическая кривая * $E(x, y, z) = y^2 z - x^3 - A x z^2 - B z^3 = 0$

#### Прямые в $\mathbb P^2_{\mathbb F_p}$ Всегда пересекаются ровно в одной точке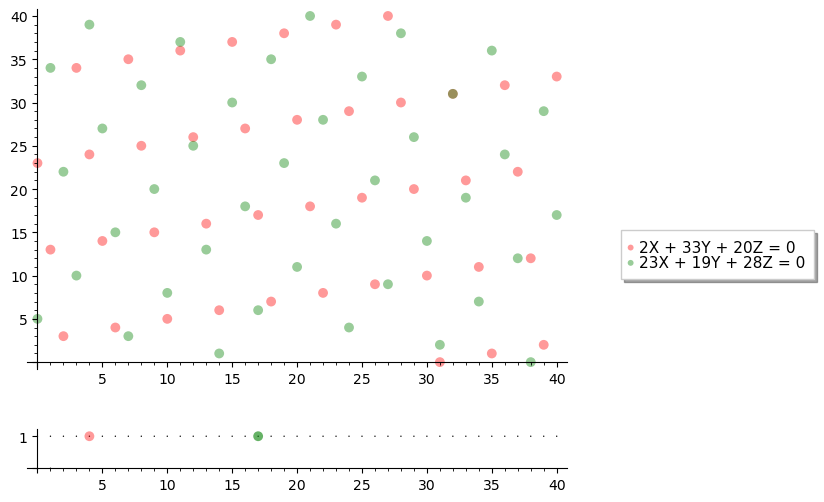 

#### Эллиптическая кривая в $\mathbb P^2_{\mathbb F_p}$ <div style="font-size: 20px"> * Для $z = 0$ всегда содержит только $(0, 1, 0)$ * $\operatorname{inv}(x, y, z) = (x, -y, z)$ * $(x, y, z) \mapsto h$ для дискретного логарифма </div>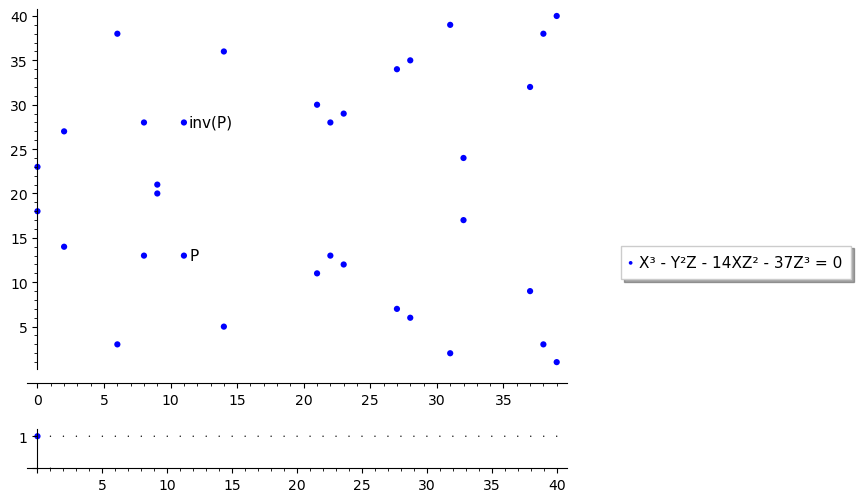 

#### Количество пересечений прямой и кривой в точке <div style="font-size: 24px"> Прямую $ax + by + cz = 0$ можно параметризовать двумя параметрами $(u, v) \neq (0, 0)$ * $x = a_1 u + b_1 v$ * $y = a_2 u + b_2 v$ * $z = a_3 u + b_3 v$ Пусть есть прямая $L(x, y, z) = \bar{L}(u, v) = 0$ $F(x, y, z) = 0$ можно преобразовать в $\bar{F}(u, v) = 0$ $\bar{F}(u, v)$ $k \ge 0$ раз пересекается в $(u_0, v_0)$ с $L$, если: * $\bar{F}(u, v) = (u_0 v - v_0 u)^k \bar{G}(u, v)$ * $\bar{G}(u_0, v_0) \neq 0$ </div>

#### Количество пересечений прямой и прямой в точке Две прямые $L_1$, $L_2$, $L_1 \neq L_2$ пересекаются в общей точке $(u_0, v_0)$ **один раз** $\bar{L_2}(u, v) = a(a_1 u + b_1 v) + b(a_2 u + b_2 v) + c(a_3 u + b_3 v)$ $\bar{L_2}(u_0, v_0) = \alpha u + \beta v = 0$ $\bar{L_2}(u, v) = \gamma (u_0 v - v_0 u)$

#### Количество пересечений прямой и эллиптической кривой Параметризуем $E(x, y, z)$ через прямую $\bar{L}(u, v)$ $\bar{E}(u, v) = \alpha u^3 + \beta v^3 + \gamma u^2 v + \delta v u^2 = 0$ $\bar{E}(u, v) = \zeta (u_0 v - v_0 u) (u_1 v - v_1 u) (u_2 v - v_2 u)$ $\bar{E}(u, v) = 0$ **в трёх точках** * $(u_0, v_0)$, $(u_1, v_1)$, $(u_2, v_2)$ Если $u_0, v_0, u_1, v_1 \in \mathbb F_p$, то $u_2, v_2 \in \mathbb F_p$

#### Групповой закон Пока предположим, что прямая c $P$ и $Q$ определена однозначно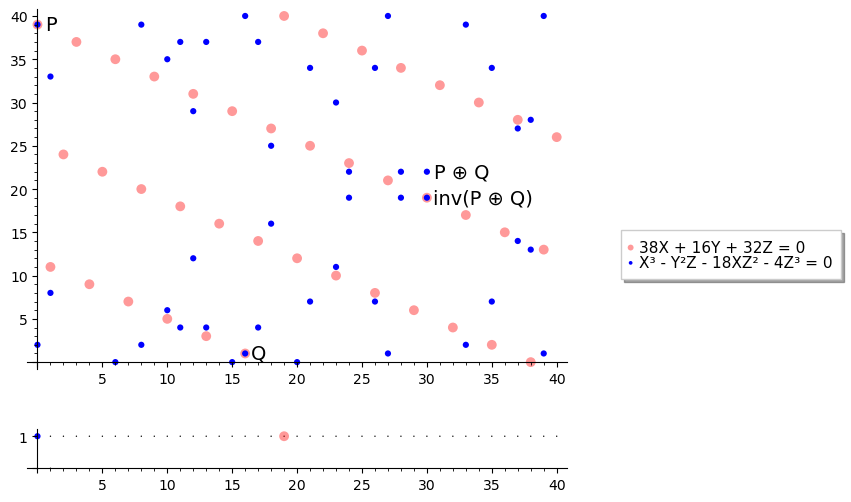 

#### Коммутативность Очевидна

#### Существование нейтрального $\mathcal O$ <div style="font-size: 24px"> * $a 0 + b 1 + c 0 = 0$, а значит, $b = 0$ * $\operatorname{inv}(P)$ лежит на той же прямой * $\operatorname{inv}(\operatorname{inv}(P)) = P$ </div>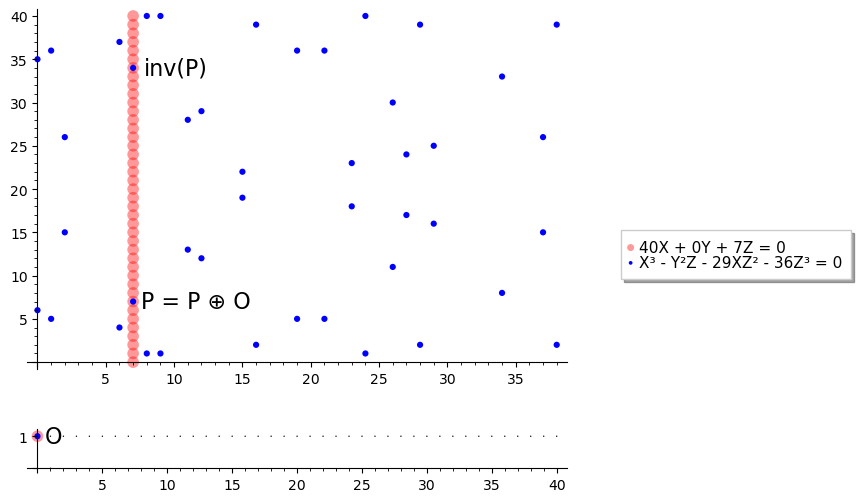 

#### Существование обратного $-P$ $-P = \operatorname{inv}(P)$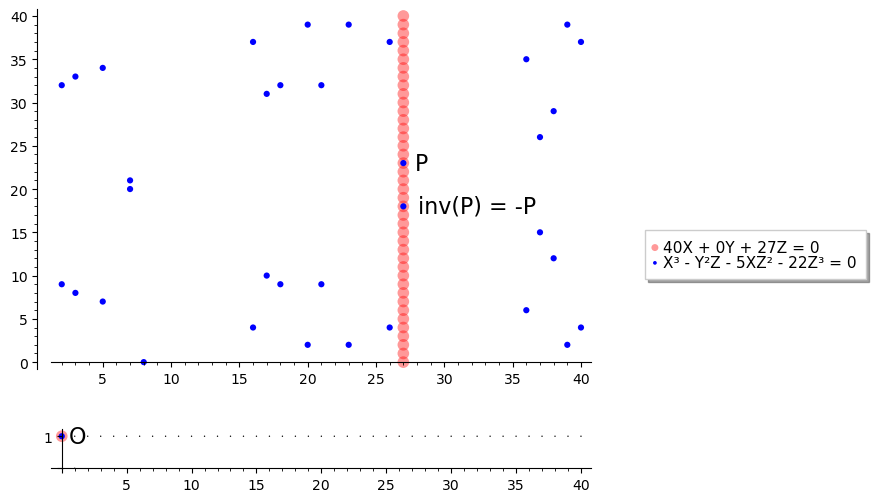 

#### Прямая через две точки: $P \oplus Q$ <div style="font-size: 32px"> $P = (x_0, y_0, z_0), Q = (x_1, y_1, z_1), P \neq Q$ $$ M = \begin{bmatrix} x_0 & y_0 & z_0 \\\\ x_1 & y_1 & z_1 \end{bmatrix} $$ $\operatorname{rank}(M) = 2$ $\dim(\operatorname{ker} M) = 1$ $L(x, y, z) = (y_0 z_1 - z_0 y_1) x + (z_0 x_1 - x_0 z_1) y + (x_0 y_1 - y_0 x_1) z$ </div>

#### Формальные частные производные $E(x, y, z) = y^2 z - x^3 - A x z^2 - B z^3$ $E_x(x, y, z) = -3 x^2 - A z^2$ $E_y(x, y, z) = 2 z y$ $E_z(x, y, z) = y^2 - 2 A x z - 3 B z^2$ Ведут себя как обычные производные (производная произведения, сложной функции...)

#### Прямая через две точки: $P \oplus P$ <div style="font-size: 18px"> * Формальная касательная в $P = (x_0, y_0, z_0)$ * $L(x, y, z) = E_x(x_0, y_0, z_0) x + E_y(x_0, y_0, z_0) y + E_z(x_0, y_0, z_0) z$ * Только она пересекает $E$ в $P$ **больше одного раза** * (доказательство опущено) </div>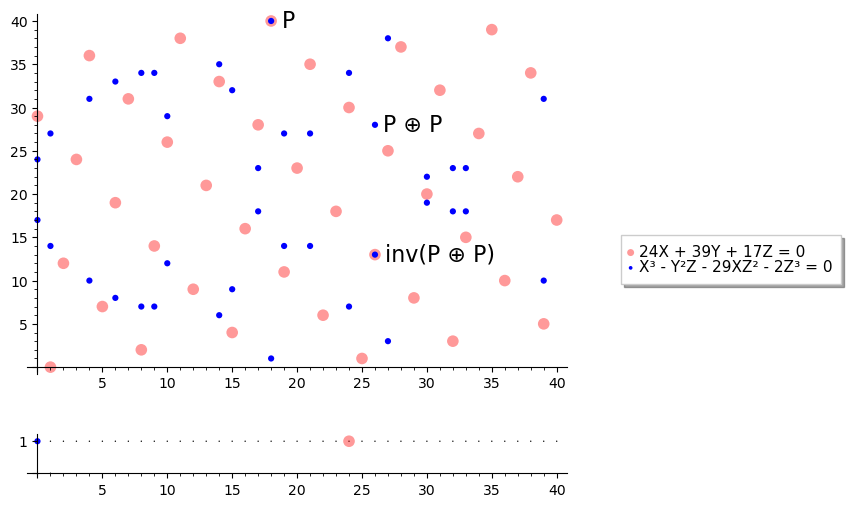 

А в $\mathcal O$ формальная касательная пересекает $E$ **три раза**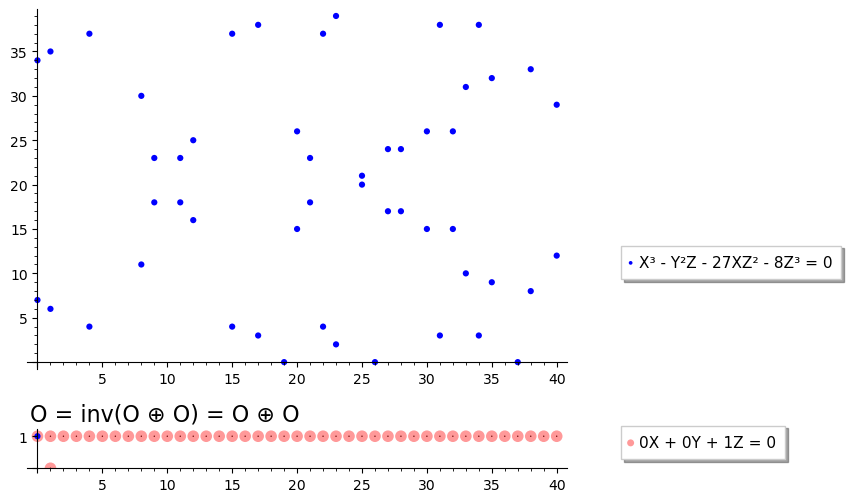 

#### Ассоциативность <div style="width: 1100px"> <table> <tr> <td> $P \oplus (Q \oplus R)$ 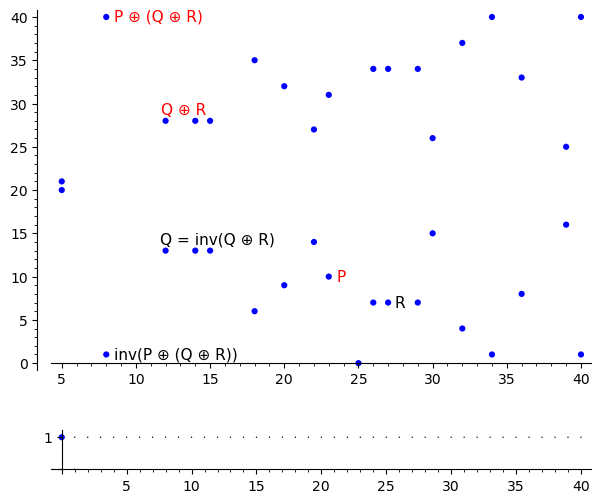 </td> <td> $(P \oplus Q) \oplus R$ 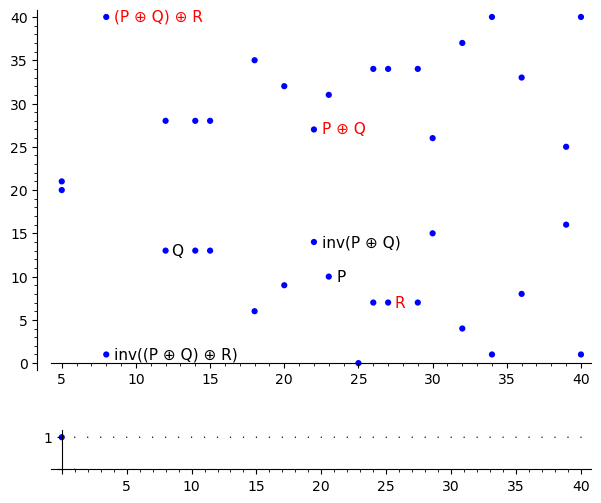 </td> </tr> </table> </div>

#### Набросок доказательства <div style="font-size: 24px"> $H(X, Y)$ — прямая через точки $X$ и $Y$ <table> <tr> <td> </td> <td> $M_1 = H(Q, R)$ </td> <td> $M_2 = H(P \oplus Q, \mathcal O)$ </td> <td> $M_3 = H(Q \oplus R, P)$ </td> </tr> <tr> <th> $L_1 = H(P, Q)$ </th> <td> $P_{11} = Q$ </td> <td> $P_{12} = \operatorname{inv}(P \oplus Q)$ </td> <td> $P_{13} = P$ </td> </tr> <tr> <th> $L_2 = H(Q \oplus R, \mathcal O)$ </th> <td> $P_{21} = \operatorname{inv}(Q \oplus R)$ </td> <td> $P_{21} = \mathcal O$ </td> <td> $P_{21} = Q \oplus R$ </td> </tr> <tr> <th> $L_3 = H(P \oplus Q, R)$ </th> <td> $P_{31} = R$ </td> <td> $P_{32} = P \oplus Q$ </td> <td> $P_{33} = \mathord{?}$ </td> </tr> <table> </div> **Лемма 1** $E(x, y, z) - \alpha M_1 M_2 M_3 - \beta L_1 L_2 L_3 = L_1 M_1 L(x, y, z)$ **Лемма 2** $L(x, y, z) = 0$ **Отсюда** $E(x, y, z) - \alpha M_1 M_2 M_3 - \beta L_1 L_2 L_3 = 0$ $E(P_{33)} = 0$